Unexpected resilience due to spatial patterns

Ecosystems are more resilient than was previously thought. They sometimes form new spatial patterns and, for that reason, can prevent tipping points from being crossed.

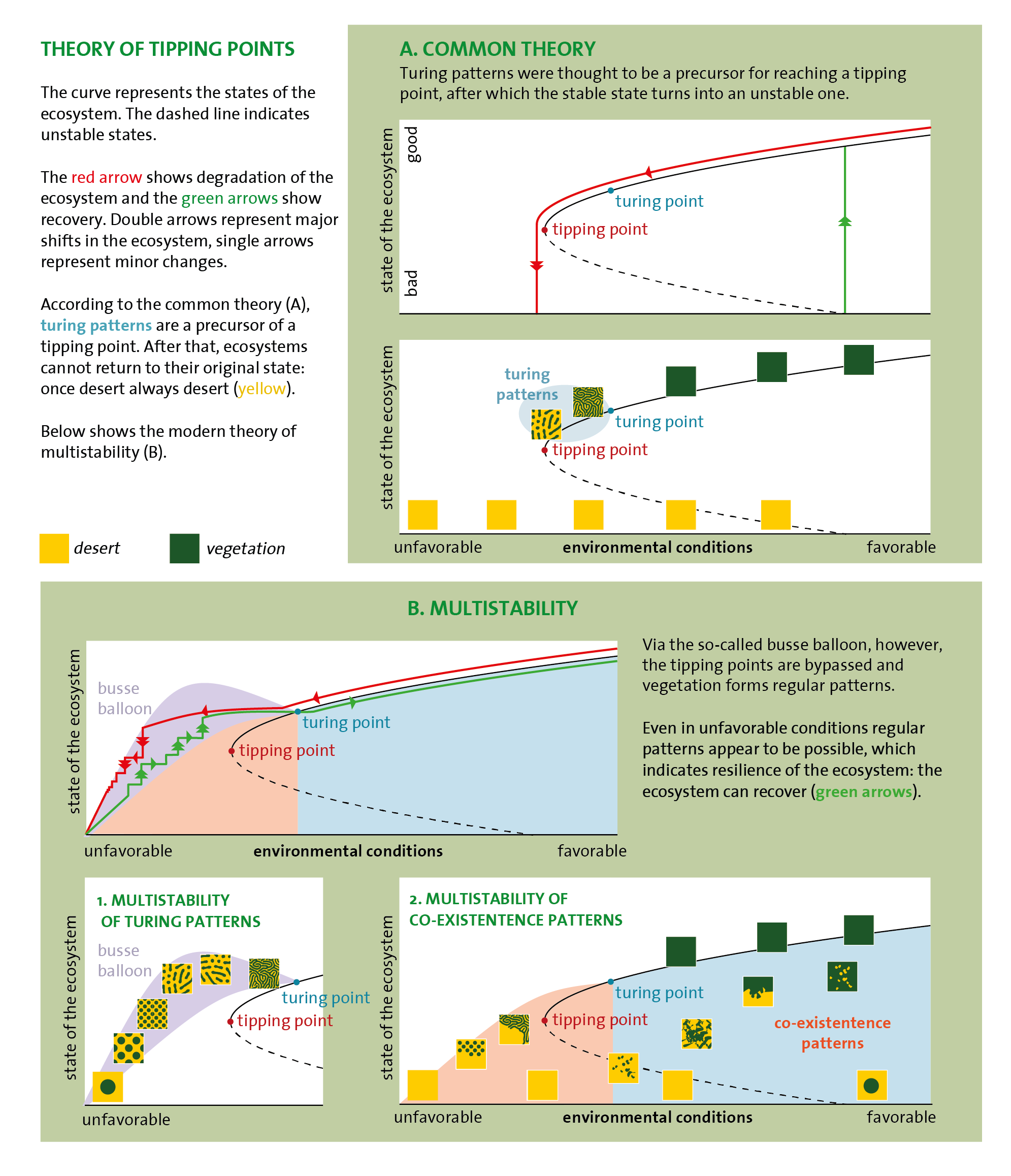
Biologists often think that ecosystems can occur in two stable, relatively unchangeable states, out of which the one can suddenly convert into the other: a healthy, desirable state reaches a tipping point and switches to a degraded, undesirable state. For instance, a tropical rainforest that, due to forest fires and logging, changes abruptly into savanna or savanna that collapses into a desert, due to overgrazing or climate change.

However, two stable states can easily coexist together within the same area. Tropical rainforest can be found next to savanna, or savanna can be interspersed with barren land. It is therefore likely that tipping points occur less often than assumed in the past. After all, it is not an entire area that tips from one state to the other but just a small part of it. Both states can apparently coexist together next to each other in a stable manner.

Also, ecosystems can occur in much more stable states than just two. That is called multi-stability. These states often occur next to each other, and together they form recognisable regular or irregular spatial patterns. That allows ecosystems to adapt easily to the new conditions and, in so doing, avoid tipping points. For example, savannas at the edge of deserts as well as close to rainforests occur in a wide range of regular and irregular spatial patterns. They have been stable there for decades even though the rainfall pattern has changed.

Turing patterns
Two types of spatial patterns can be distinguished. The regular Turing patterns – named after the English mathematician Alan Turing who was the first to predict these – and the irregular coexistence patterns. The Turing patterns arise if, due to a disturbance, a homogenous ecosystem – a continuous stretch of forest or savanna, for instance – disintegrates into patches of vegetation that appear to be regular spots, labyrinths, stripes or gaps when viewed from space. The coexistence patterns consist of two different stable states, but in this case they occur interspersed and irregular next to each other in the same area with sharp boundaries between them, such as a tropical rainforest interspersed with savanna.

These new insights are due to mathematical modelling studies and new satellite observations and have recently led to a change in the tipping point theory. Scientists previously thought that Turing patterns were an early warning signal for approaching a tipping point and thus an indicator for the ecosystem’s vulnerability. In the case of crossing such tipping point, the dots or stripes of vegetation would disappear abruptly and a completely homogenous desert would arise.

Avoiding tipping points
However, these patterns appear to provide resilience instead: they make it possible to avoid tipping points. The ecosystem adapts in such a way that it remains within the conditions or parameter space that in mathematics is referred to as the ‘Busse balloon’, named after the German physicist Friedrich Busse. For example, even if the rainfall decreases, the vegetation still continues to exist. The number of spots or strips adapts and forms a new regular pattern. Not all of the vegetation disappears, but just a few spots or stripes. Irregular coexistence patterns can also form due to local disturbances, in which two stable states can continue to coexist together. If the circumstances change, then these coexistence patterns can subsequently disintegrate again into regular Turing patterns.

© Stichting Biowetenschappen en Maatschappij

More leads to even more
But how does that work? And what makes ecosystems more resilient than was previously thought? Tipping points occur due to positive feedback – changes that automatically lead to an even faster change in the same direction. In other words, more leads to even more, or less leads to even less. An example is the phenomenon of vegetation attracting water: the more vegetation, the easier it is for rainwater to infiltrate into the soil and be retained, as a result of which even more vegetation grows, and so forth. The same positive feedback also works the other way: less vegetation means that the soil retains less water, as a result of which less vegetation survives until eventually, all that remains is a desert. Consequently, a positive feedback can lead to tipping point.

Conversely, negative feedbacks do something else: they delay or attenuate changes. They therefore lead to stability and resilience. An example of that is if too many plants grow in the same space and, as a result, inhibit each other’s growth because they share the same resources such as water and light. As a consequence an equilibrium is reached. If a disturbance occurs – such as grazing or fire – then the plants are thinned out, after which they will grow back again to reach the original equilibrium. This is a change in the opposite direction: less leads to more, or more leads to less.

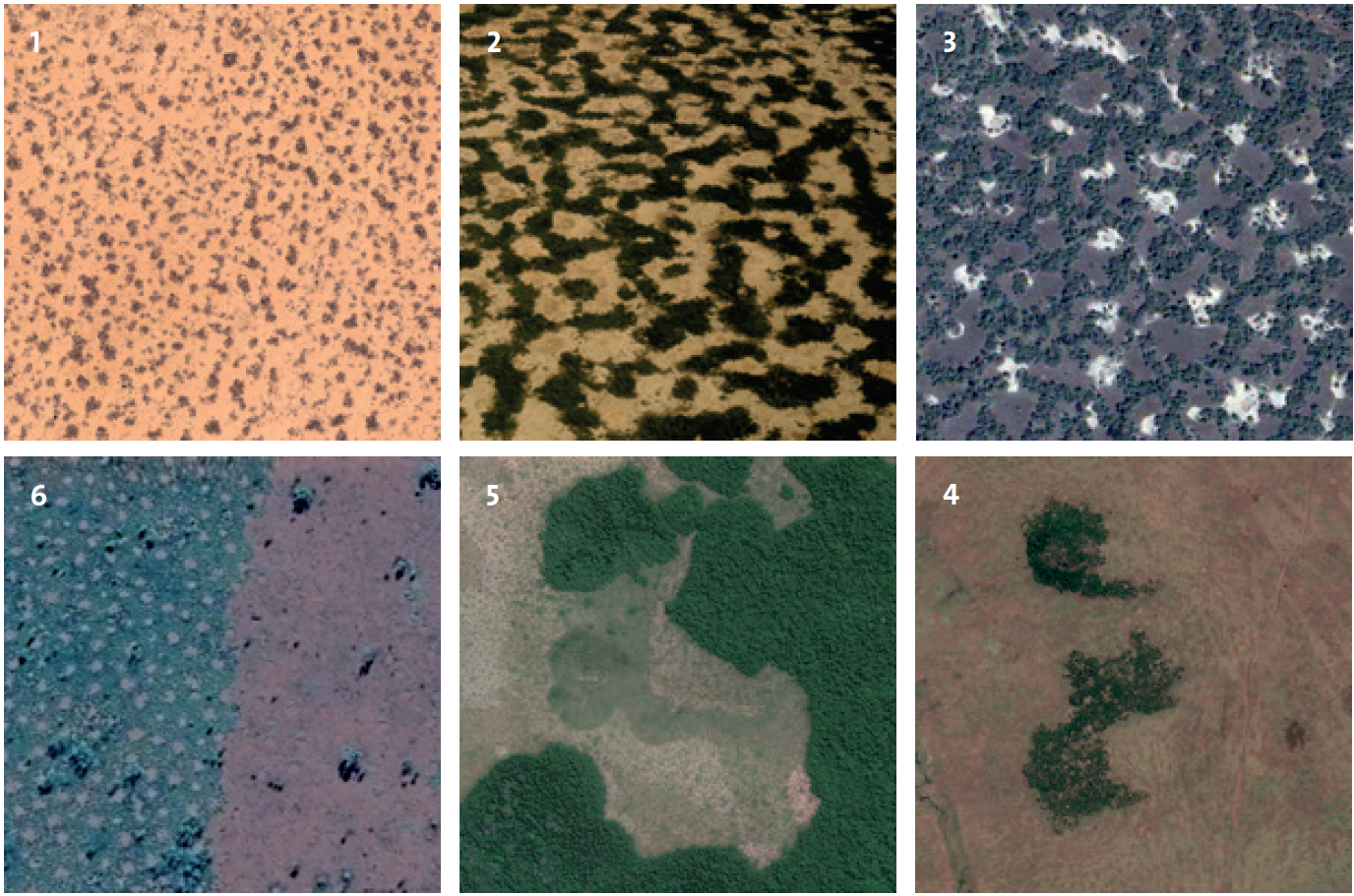
Google Earth images of Turing patterns, coexistence patterns and combinations of these. Clockwise from the top left: Turing patterns (dots) of savanna and barren land in Sudan, Turing pattern (labyrinth) of savanna and barren land in Niger, Turing pattern (labyrinth) of trees and grassland in Mali, coexistence pattern of forest and grassland in Kenya, coexistence pattern of tropical rainforest and savanna in Gabon, coexistence pattern of barren land and savanna with Turing pattern (gaps) in Australia.

Small and large scale
The Turing patterns arise due to the simultaneous occurrence of a positive feedback on a small scale, and a negative feedback on a larger scale. Consider, for instance, a savanna at the edge of the desert. Plants cannot cover the entire surface here because there is too little water for that. Where vegetation is already present, water infiltrates into the soil more easily and, for this reason, it is easier for the vegetation to grow further – a positive feedback. However, as a result of this, it becomes even drier at the spots without vegetation further away since, as remarked above, there is not enough water for the entire area. That therefore hinders the growth of vegetation in places that have so far remained uncovered – the negative feedback.

This so-called scale-dependent feedback provides stability and resilience. Due to the negative feedback, a sort of ‘waterbed effect’ arises. This is because such a change in the opposite direction also has the consequence that a decrease in vegetation at one location leads to an increase of vegetation at another location further away. Scale-dependent feedback is a general mechanism that frequently occurs in ecosystems. Not just in savannas but also in coral reefs, peat bog areas, grasslands, seagrass fields and salt marshes. The spatial availability of water can be a driving force, but also the spread of nutrients such as nitrogen and phosphate and other sources of food such as algae. Therefore, Turing patterns are omnipresent in nature.

Sharp boundary
Irregular coexistence patterns are probably even more common than Turing patterns, because they can already be formed due to frequently occurring local disturbances, such as fire or grazing. One such example is a savanna that is maintained by burning, which exists next to a tropical rainforest that cannot burn due to a lack of dry grass. In this way, a sharp boundary can occur, and both the savanna and tropical rainforest can persist. This implies that ecosystems that were so far thought to be sensitive to tipping points are, in fact, more resilient. On the other hand, the formation of patterns does not necessarily exclude the occurrence of tipping points. The conditions under which tipping points do or do not occur should therefore be investigated further.

All of this not only applies to ecosystems, but also to other complex systems such as the warm Gulf Stream, the icecaps at the poles and even the Earth system as a whole. These systems possibly respond to changes with positive and negative feedback and spatial pattern formation as well. Each complex system that is relatively large enough compared to the scale of the spatial patterns that it can form, can possibly avoid tipping points too. Remaining questions are : for which complex systems is this applicable, and at which spatial scale? And for which systems does this not hold?